This is an old revision of the document!
Table of Contents
Different Power Gains
Types of power gain
If you hear the word 'power gain', you justly interpret this as the ratio of the output power $P_{out}$ to the input power $P_{in}$:
$$ gain=\frac{P_{out}}{P_{in}}$$
Unfortunately, confusion is possible, since there are different ways to define the ouput and input power. And depending on which definition of power you use, you get another value for the gain. But mankind has found a solution: we use different names for the gains, depending on which power is considered. Let us try to give an overview of the three most common gains.
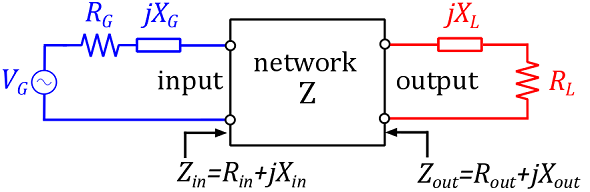
A two-port network, connected to a source and a load.
Consider a network $Z$ with one input and one output (a two-port network). The input is connected to a generator (a voltage source $V_G$ with internal impedance $Z_G=R_G+j.X_G$) and the output to a load impedance $Z_L=R_L+j.X_L$.
- We call the input impedance of the network $Z_{in}=R_{in}+j.X_{in}$. Note that the input impedance $Z_{in}$ is dependent on $Z_L$ (see figure 1).
- We call the output impedance $Z_{out}=R_{out}+j.X_{out}$. Note that the output impedance $Z_{in}$ is dependent on $Z_G$ (see figure 1).
Figure 1: A network Z is connected to a generator at the input, and a load at the output
We will define three different types of gain for the network Z. We first start by considering two different definitions of input power.
Different types of input power
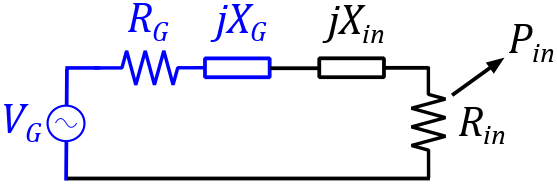
Actual input power $P_{in}$
The actual input power $P_{in}$ (usually simply called 'the input power') is the power that the generator delivers to the network $Z$, connected to a load $Z_L$. It is the power dissipated in $R_{in}$ as seen in the following figure.
Figure 2: Definition actual input power
As a result, the input power is dependent not only on the network $Z$, but also on the value of $Z_L$. It is independent on $Z_G$.
This implies that a load impedance $Z_L$ must be explicitly specified in order to be able to define the actual input power $P_{in}$.
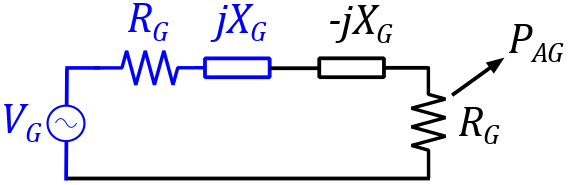
Available input power $P_{AG}$
The available input power $P_{AG}$ (often called 'the available input power of the generator') is the maximum input power that can be put into the network $Z$ by a generator. This is achieved for a specific value of the load, i.e., if the load value is chosen so that the input impedance $Z_{in}$ of the network is matched (= equal resistance, opposite reactance) to the generator impedance $Z_G$.
Figure 3: Definition available input power
The available input power for the network is only dependent on the value of $Z_G$. It is independent on the network $Z$ or $Z_L$ since both are together matched to the generator impedance.
This implies that the generator impedance must be specified in order to be able to define the available input power.
Different types of output power
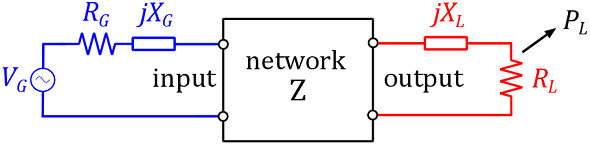
The power delivered to the load $P_{L}$
It is the power dissipated in the load ZLas seen in the following figure.
Figure 4: Definition power delivered to the load
Note that $P_L$ is dependent on the value of the load and not on the generator impedance. This implies that a load impedance $Z_L$ must be explicitly specified in order to be able to define $P_L$.
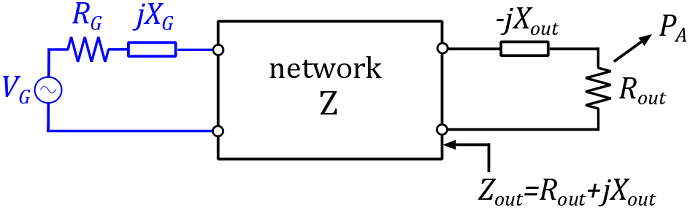
The maximum available load power $P_{A}$
The maximum available load power $P_A$ is the maximum power that can be dissipated into the load. This is realized for a specific value of the load, i.e., if the load value is chosen so that the output impedance $Z_{out}$ of the network is matched (= equal resistance, opposite reactance) to the load impedance $Z_L$. In other words, the maximum available load power is the power the network delivers to a load that is matched to its output impedance.
Figure 5: Definition maximum available load power