This is an old revision of the document!
Table of Contents
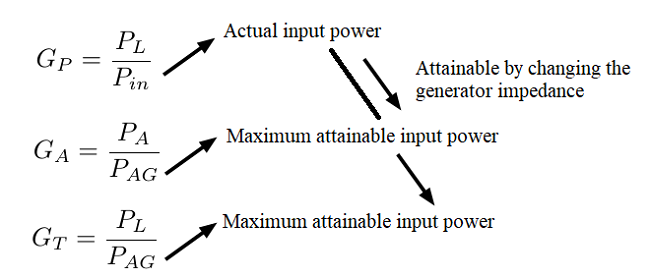
Different Power Gains
Types of power gain
If you hear the word 'power gain', you justly interpret this as the ratio of the output power $P_{out}$ to the input power $P_{in}$:
$$ gain=\frac{P_{out}}{P_{in}}$$
Unfortunately, confusion is possible, since there are different ways to define the ouput and input power. And depending on which definition of power you use, you get another value for the gain. But mankind has found a solution: we use different names for the gains, depending on which power is considered. Let us try to give an overview of the three most common gains.
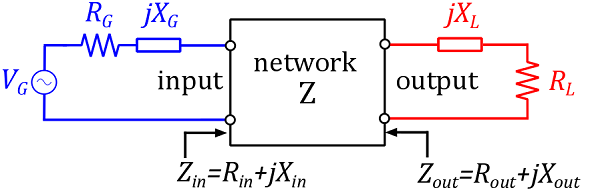
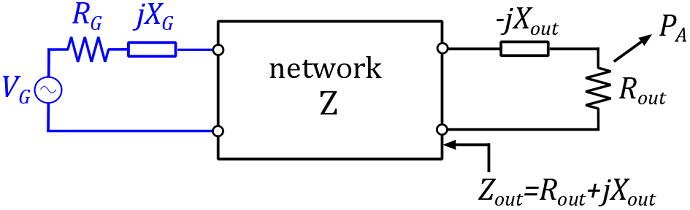
A two-port network, connected to a source and a load.
Consider a network $Z$ with one input and one output (a two-port network). The input is connected to a generator (a voltage source $V_G$ with internal impedance $Z_G=R_G+j.X_G$) and the output to a load impedance $Z_L=R_L+j.X_L$.
- We call the input impedance of the network $Z_{in}=R_{in}+j.X_{in}$. Note that the input impedance $Z_{in}$ is dependent on $Z_L$ (see figure 1).
- We call the output impedance $Z_{out}=R_{out}+j.X_{out}$. Note that the output impedance $Z_{in}$ is dependent on $Z_G$ (see figure 1).
Figure 1: A network Z is connected to a generator at the input, and a load at the output
We will define three different types of gain for the network Z. We first start by considering two different definitions of input power.
Different types of input power
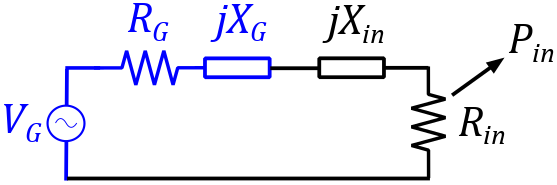
Actual input power $P_{in}$
The actual input power $P_{in}$ (usually simply called 'the input power') is the power that the generator delivers to the network $Z$, connected to a load $Z_L$. It is the power dissipated in $R_{in}$ as seen in the following figure.
Figure 2: Definition actual input power
As a result, the input power is dependent not only on the network $Z$, but also on the value of $Z_L$. It is independent on $Z_G$.
This implies that a load impedance $Z_L$ must be explicitly specified in order to be able to define the actual input power $P_{in}$.
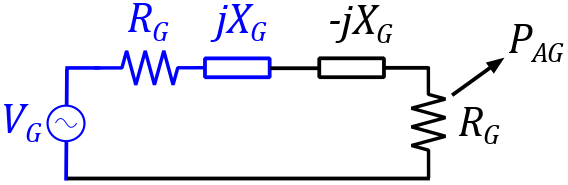
Available input power $P_{AG}$
The available input power $P_{AG}$ (often called 'the available input power of the generator') is the maximum input power that can be put into the network $Z$ by a generator. This is achieved for a specific value of the load, i.e., if the load value is chosen so that the input impedance $Z_{in}$ of the network is matched (= equal resistance, opposite reactance) to the generator impedance $Z_G$.
Figure 3: Definition available input power
The available input power for the network is only dependent on the value of $Z_G$. It is independent on the network $Z$ or $Z_L$ since both are together matched to the generator impedance.
This implies that the generator impedance must be specified in order to be able to define the available input power.
Different types of output power
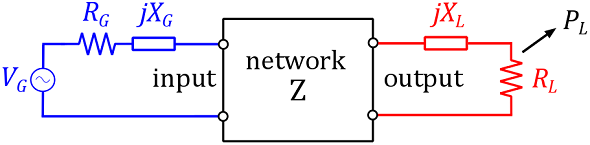
The power delivered to the load $P_{L}$
It is the power dissipated in the load ZLas seen in the following figure.
Figure 4: Definition power delivered to the load
Note that $P_L$ is dependent on the value of the load and not on the generator impedance. This implies that a load impedance $Z_L$ must be explicitly specified in order to be able to define $P_L$.
The maximum available load power $P_{A}$
The maximum available load power $P_A$ is the maximum power that can be dissipated into the load. This is realized for a specific value of the load, i.e., if the load value is chosen so that the output impedance $Z_{out}$ of the network is matched (= equal resistance, opposite reactance) to the load impedance $Z_L$. In other words, the maximum available load power is the power the network delivers to a load that is matched to its output impedance.
Figure 5: Definition maximum available load power
The maximum available load power $P_A$ for the network is dependent on the value of $Z_G$ and the network $Z$. It is independent on the load $Z_L$.
This implies that the generator impedance must be specified in order to be able to define $P_A$.
Three different power gains
It is now possible to define different power gains, depending on which definition of input and output power is chosen. We will limit ourselves to the three most common power gains.
The operating power gain $G_{P}$
The operating power gain $G_P$ (often simply called 'the power gain' or 'actual gain') is defined as the ratio of the power dissipated in the load $Z_L$ to the power that the generator delivers to the network $Z$, connected to that load $Z_L$:
$$ G_P=\frac{P_{L}}{P_{in}}$$
Since both $P_L$ and $P_{in}$ are independent on the generator impedance $Z_G$, the operating power gain $G_P$ is also independent on $Z_G$. The generator impedance does not need to be specified: we just need to know how much power got to the network, not how it got there.
The gain depends on the network $Z$ and on the load value $Z_L$. Obviously, $G_P$ can only be defined if a value for the load $Z_L$ is specified.
In systems where the goal is to transfer energy from a source to a load, the operating power gain is often called 'the power conversion efficiency', or simply 'the efficiency“ of the system.
Available gain $G_{A}$
The available gain $G_A$ is defined as the ratio of the maximum available load power $P_A$ to the available input power $P_{AG}$:
$$ G_A=\frac{P_{A}}{P_{AG}}$$
Since both $P_A$ and $P_{AG}$ are independent on the load impedance $Z_L$, the available gain $G_A$ is also independent on $Z_L$. The gain depends on the network $Z$ and on the generator impedance value $Z_G$.
Obviously, $G_A$ can only be defined if a value for the generator impedance $Z_G$ is specified.
Transducer gain $G_{T}$
The transducer gain $G_T$ is defined as the ratio of the power dissipated in the load $Z_L$ to the available input power $P_{AG}$ of the generator:
$$ G_T=\frac{P_{L}}{P_{AG}}$$
It is dependent on both the load impedance $Z_L$ and the generator impedance $Z_G$. Both have to be specified in order to be able to define the transducer gain $G_T$.
Overview output power within the gains
Overview input power within the gains
Simulation example
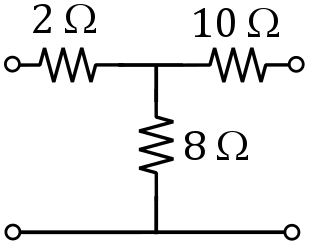
As example, let us consider a very simple, purely resistive network, consisting of three resistors:
Figure 6: Simple, purely resistive, example network
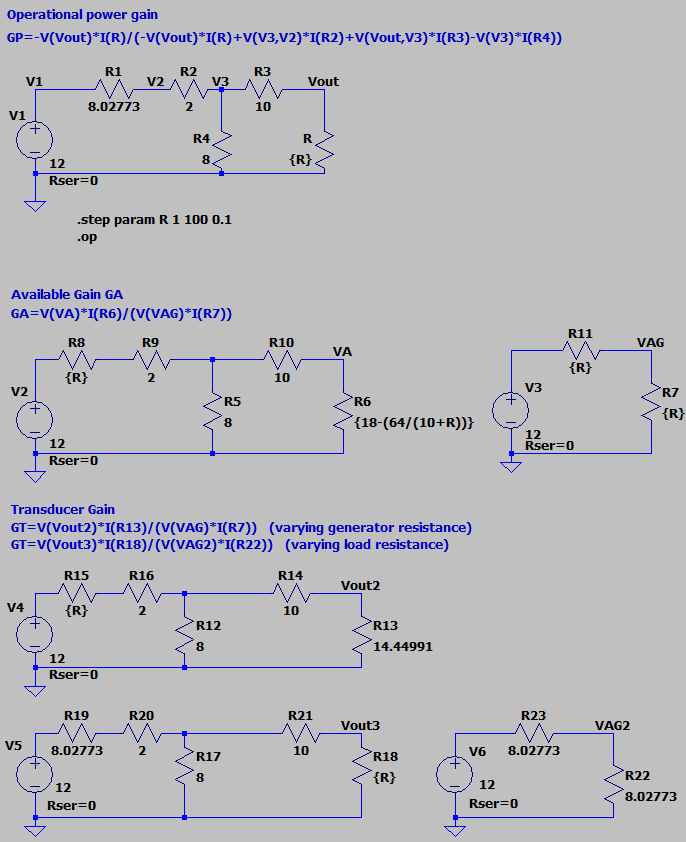
We simulate the three gains in LT Spice with a DC voltage source of 12 V, as function of the generator resistance and the load resistance.
Figure 7: Schematics in LT Spice for the three gains, for the example network, with variable load and/or generator resistance {R}.
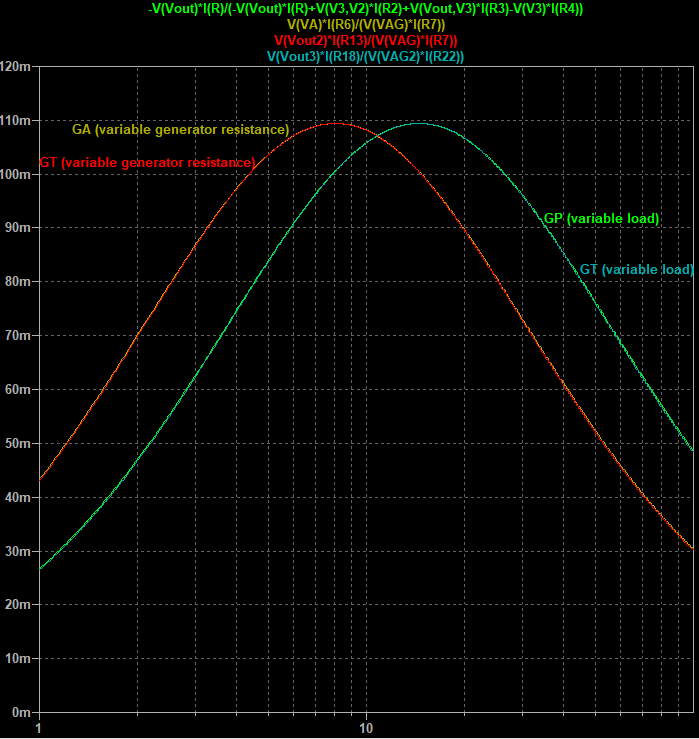
We first simulate the operating power gain $G_P$ as function of the load resistance. This gain is independent on the generator resistance. In the simulation, a generator resistance of 8.02773 ohm was chosen (see further), but this value doesn't matter for the simulation of the operating power gain $G_P$.
The graph below (green) shows that a maximum of $G_P$ = 10.9% is reached for a load of 14.5 ohm.
Figure 8: Simulation results of the gains as function of varying generator or load resistance (logarithmic axis) for the given example.
Next, the available gain $G_A$ is simulated as function of varying generator resistance (this gains is independent on the value of the load). We find a maximum of 10.9% at a generator resistance of 8.0 ohm.
Finally, the transducer gain $G_T$ is simulated, first for varying generator resistance, and next for varying load. The generator/load resistance in each non-varying case is chosen to be the optimal value for the other gains. The graphs are identical to the other gains (explanation). A maximum of 10.9% is found for the optimal generator and load resistance of 8.0 and 14.5 ohm.
Some background references
- Egan,W.F. Practical RF System Design; JohnWiley & Sons: Hoboken, NJ, USA, 2003; pp. 313–315.
- Mastri, F.; Mongiardo, M.; Monti, G.; Dionigi, M.; Tarricone, L. Gain Expressions for Resonant Inductive Wireless Power Transfer Links with One Relay Element. Wireless Power Transfer 2018, 5, 27–41.
- Ben Minnaert, Giuseppina Monti, Alessandra Costanzo and Mauro Mongiardo, Gain Expressions for Capacitive Wireless Power Transfer with One Electric Field Repeater. Electronics 2021, 10, 723.