Wireless Power Wiki

The relationship between the voltage $v_C$ over and the current $i_C$ through a capacitor is determined by its capacitance $C$:

$$ i_C(t)=C\frac{dv_C(t)}{dt}$$

However, this current-voltage relationship is not valid when the capacitor is varying in time. For a time variant capacitor, the equation modifies to:

$$ i_C(t)=\frac{d}{dt}[C(t).v_C(t)]=C(t)\frac{dv_C(t)}{dt}+v_C(t)\frac{dC(t)}{dt}$$

Rearranging this equation gives an expression for the voltage over the capacitor:

$$ v_C(t)=\frac{1}{C(t)}[C(0)v_C(0)+\int_0^t i_C(t) dt] $$

valid if $C(t)\neq 0$ at any time.

We will use this expression to simulate a time-varying capacitor in LT Spice. Notice the limitation that $C(t)\neq 0$ at any time.

Suppose we want we simulate a sinusoidal value in function of time with a certain offset: $C(t)$= 5 nF + 3 nF.sin(2π.100 kHz.t). In order to realize this, we have to introduce a custom component in SPICE with the following subcircuit:

.subckt capacitor + - params: VC0=0
.func C(time) {5n+3n*sin(2*pi*100k*time)}
hvolt + - value={(sdt(I(hvolt))+VC0*C(0))/C(time)}
.ends

Current Dependent Voltage Source

The voltage over the capacitor (see equation above) is modeled via a current dependent voltage source hvolt. The integral is realized via the sdt function in SPICE. The initial value at time t=0 of the capacitor must be given as parameter.

First, we save the code for this subcircuit into a .txt-file and, for example, place this file in the same folder as your SPICE circuit file.

Next, open the text file in LT Spice, right click on the first word “.subckt”, and select “Create symbol”.

The program asks you if you wish to automatically create a symbol. Click “yes”. A .asy file is created which contains your custom time-varying capacitor, typically in the folder 'C:Users\YourUserName\AppData\Local\LTspice\lib\sym\AutoGenerated'

To use the time-varying capacitor in a circuit, click “component” (F2) and insert the custom capacitor by searching “capacitor” in the window.

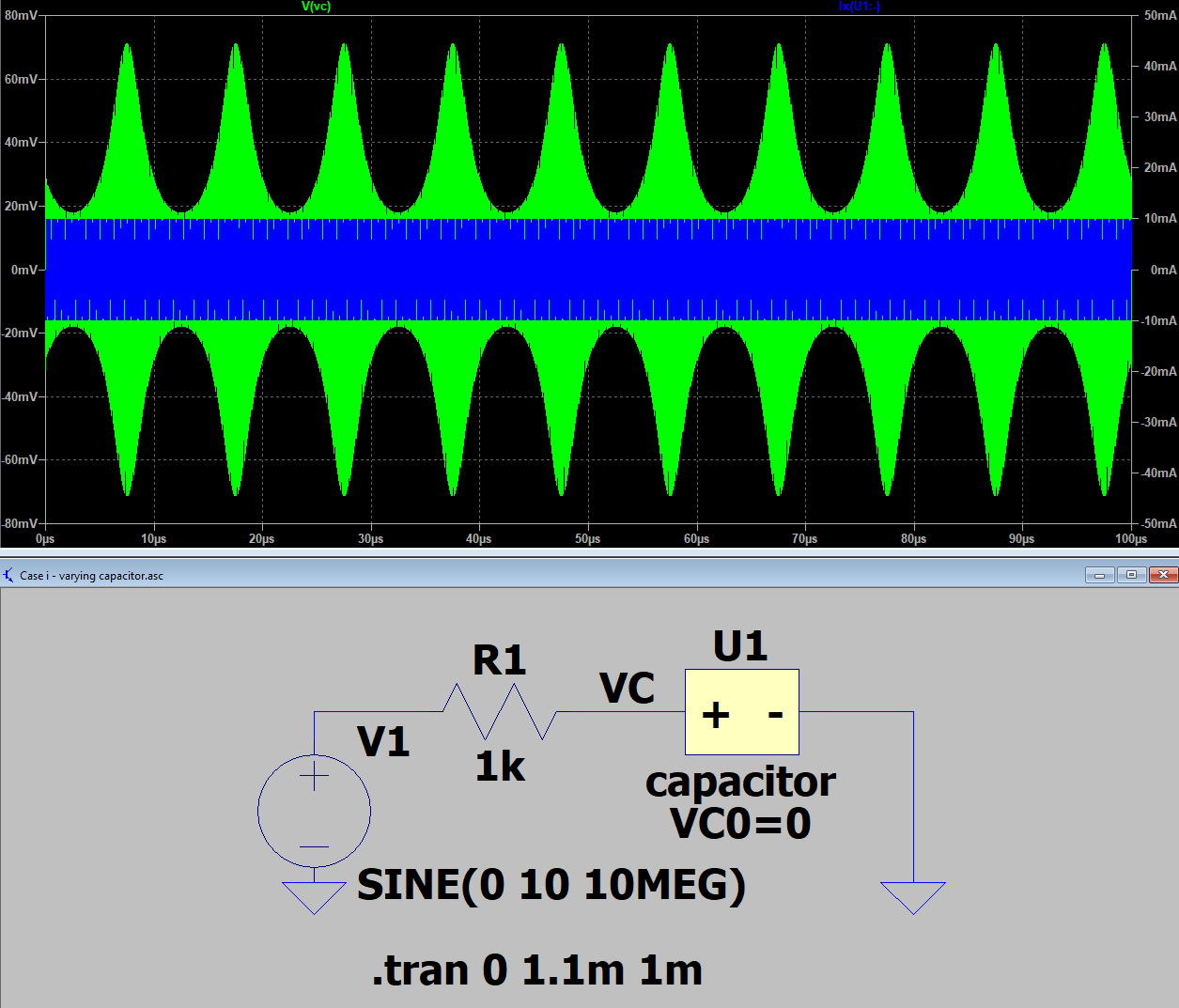
Plotting the value of the capacitance in SPICE in function of time is not straightforward. Let us just check some individual times: we compare the value of the current through and voltage over the capacitor (i) in the case of the time-varying capacitor at time $t_i$ (after the transition period), and (ii) in the case of a static capacitor with value $C(t_i)$.

Case (i): We apply a high frequency source in order to create an envelope facilitating comparison between both cases.

At a certain time, e.g., t=50µs, the value of the capacitor equals $C$(50µs)= 5 nF + 3 nF.sin(2π.100 kHz.50µs)=5 nF. If we then zoom in at the simulation at t=50µs, we find the peak value of voltage over and current through the inductor.

Case (ii): We compare this value with a static inductor of 5 nF:

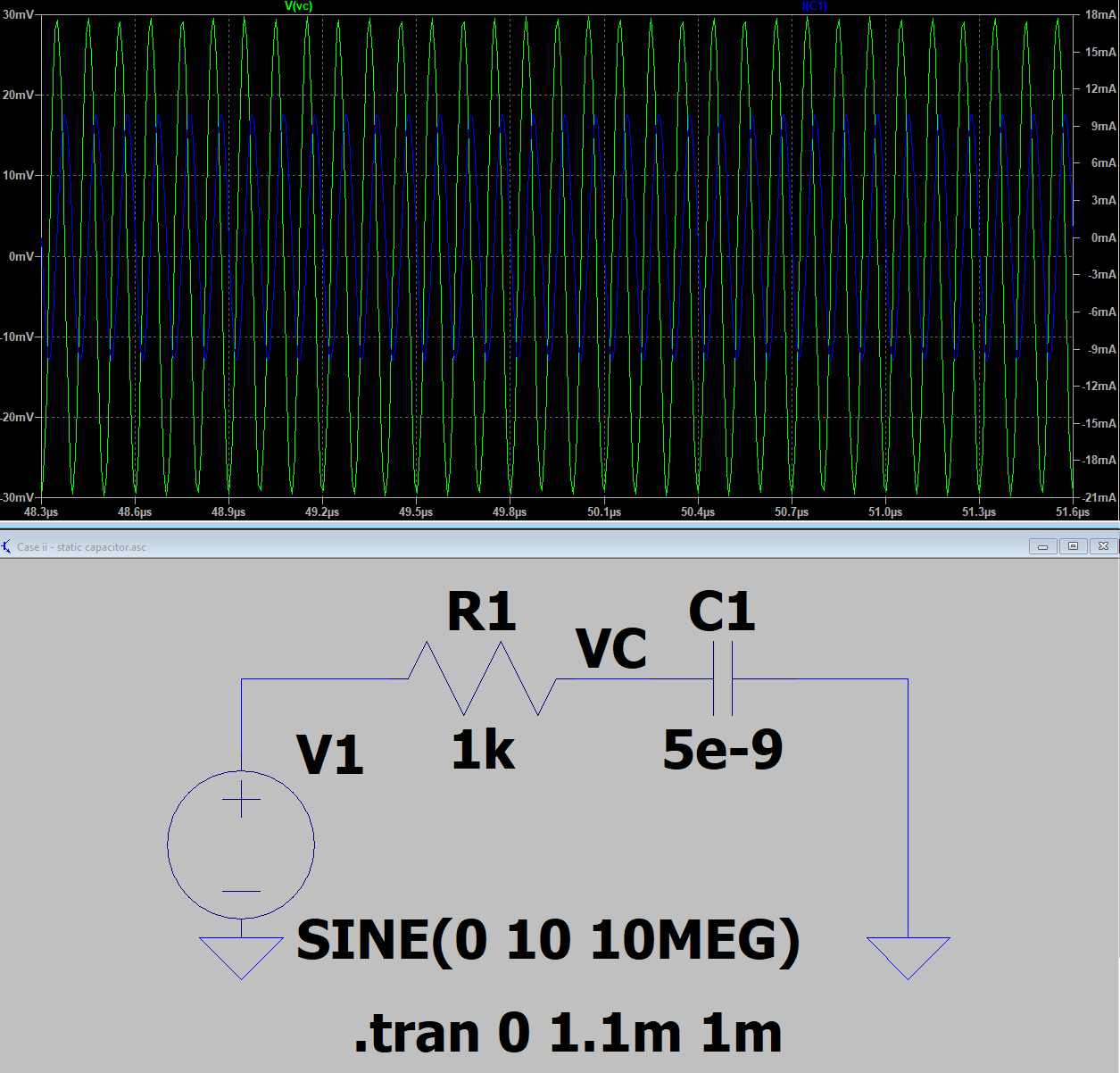
We find that both the current and voltage correspond to case (i).

We do the same for a lot of other values of time, and always find a correspondence between both cases. This is not a rigid proof, but it gives us sufficient confidence that the capacitor was modeled correctly in SPICE.

References

• Biolek, D., Kolka, Z., & Biolkova, V. (2007). Modeling time-varying storage components in PSpice. In Proc. Electronic Devices and Systems IMAPS CS International Conference EDS (Vol. 2007, pp. 39-44).